nms非极大抑制

非极大值抑制顾名思义就是抑制不是极大值的元素，搜索局部的极大值。这个局部代表的是一个邻域，邻域有两个参数可变，一是邻域的维数，二是邻域的大小。这里不讨论通用的NMS算法，而是用于在目标检测中用于提取分数最高的窗口的。例如在行人检测中，滑动窗口经提取特征，经分类器分类识别后，每个窗口都会得到一个分数。但是滑动窗口会导致很多窗口与其他窗口存在包含或者大部分交叉的情况。这时就需要用到NMS来选取那些邻域里分数最高（是行人的概率最大），并且抑制那些分数低的窗口。

IOU

nms主要是基于一个评价指标，IOU，简单来讲就是模型产生的目标窗口和原来标记窗口的交叠率。具体我们可以简单的理解为： 即检测结果(DetectionResult)与 Ground Truth 的交集比上它们的并集，即为检测的准确率 IoU :

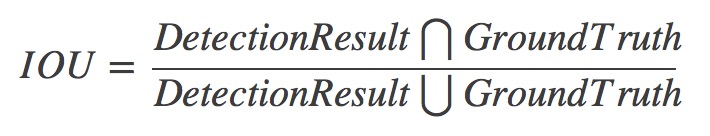
具体就如下图所示，iou = (area1 + area2) / inter_area

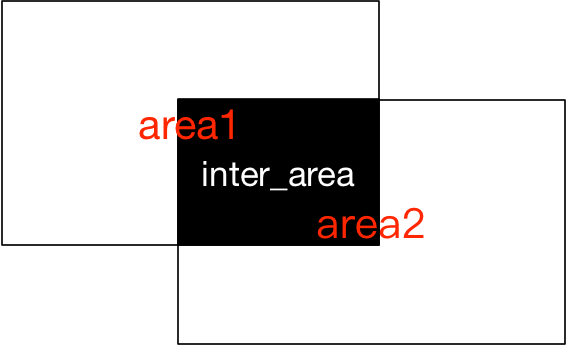
矩形的iou很好算，代码也很好写，网上代码很多，就不介绍了。

不规则四边形的nms

虽然矩形也是四边形，也有四个点，但矩形很特殊。虽然矩形有4个点，但它只有4个值[xmin, xmax, ymin, ymax]，只需要知道这四个值就可以确定一个矩形了。所以对于矩形而言并没有多少情况需要考虑，而四边形不一样，四边形需要8个值，[x1, y1, x2, y2, x3, y3, x4, y4]，所以它的情况比较复杂。

四边形IOU计算

首先我们要先知道在已知4个点的坐标情况下，如何计算一个四边形的面积，这里我是将它分成两个三角形然后用公式求解。这个函数当然不只可以求四边形面积，它计算的是多边形的面积。

typedef struct point_sh{
    int x,y;
    float sina;
    int q;
}Point;

inline int compute_q(std::vector<point_sh>& pt, float x0, float y0)
{
    for (int i=0; i<pt.size(); i++)
    {
        point_sh*p = &pt[i];
        if (p->x - x0 > 0)
        {
            if (p->y - y0 > 0)
                p->q = 1;
            else
                p->q = 4;
        }
        else
        {
            if (p->y - y0 > 0)
                p->q = 2;
            else
                p->q = 3;        
        }
    }

    return 0;
}

float polygon_area(std::vector<point_sh> pt)
{
    if (pt.size() < 3)
        return -100;

    float x0,y0;
    x0 = (pt[0].x + pt[1].x + pt[2].x) / 3.0;
    y0 = (pt[0].y + pt[1].y + pt[2].y) / 3.0;
    //std::vector<float> sins;
    float dx, dy, ds, sina;
    for (int i=0; i<pt.size(); i++)
    {
        dx = pt[i].x - x0;
        dy = pt[i].y - y0;
        ds = std::sqrt(dx * dx + dy * dy);
        pt[i].sina = dy / ds;
    }

    compute_q(pt, x0, y0);
    //简单排序，如有需要可以优化
    int j=0;
    while(1)
    {
        if (j > pt.size())
            break;

        for (int i=1; i<pt.size(); i++)
        {
            if (pt[j].q < pt[i].q)
                continue;
            
            if (pt[j].q > pt[i].q)
                std::swap(pt[j], pt[i]);
            else if ((pt[j].q == 1 || pt[j].q == 4) && pt[j].sina > pt[i].sina ||
                     (pt[j].q == 1 || pt[j].q == 4) && pt[j].sina < pt[i].sina)
                        std::swap(pt[j], pt[i]);
        }
        j++;
    }

    point_sh Fpt = pt[0];
    float area = 0;
    for (int i=1; i<pt.size()-1; i++)
    {
        area += std::fabs(0.5f * (Fpt.x * (pt[i].y - pt[i+1].y) + pt[i].x * (Fpt.y - pt[i].y) + pt[i+1].x * (pt[i+1].y - Fpt.y)));
    }

    return area;
}

这样，其实两个四边形的面积就可以直接求出来了，也就是area1 + area2的值，接下来需要找出两个四边形的相交区域的顶点，这部分代码我主要参考了 https://www.cnblogs.com/dwdxdy/p/3232110.html

同理得到顶点集合后直接代入函数即可得到交集面积。

float polygon_iou(bbox polygon1, bbox polygon2)
{
    float iou, inter_area, area1, area2;
    std::vector<point_sh> ps1, ps2;
    ps1 = poly2point(polygon1);
    ps2 = poly2point(polygon2);
    std::vector<Point> inter_poly;
    if (PolygonClip(ps1, ps2, inter_poly))
    {
        area1 = polygon_area(ps1);
        area2 = polygon_area(ps2);
        inter_area = polygon_area(inter_poly);
        iou = inter_area / (area1 + area2);
    }
    else
        iou = 0;
    return iou;
}

nms

nms的话还是要先根据框的分数(score)来确定一个基准框，然后再计算iou来消除其他的框。

bool compare(bbox a, bbox b)
{
    return a.score < b.score;
}

static int nms(std::vector<bbox>& polygons, float overlap)
{
    std::sort(polygons.begin(), polygons.end(), compare);
    int j=0;
    while(1)
    {
        bbox Fpolygon = polygons[j];//try..catch
        j++;
        if (j > polygons.size())
            break;
        
        for (int i=j; i<polygons.size(); i++)
        {
            float iou = polygon_iou(Fpolygon, polygons[i]);
            if (iou > overlap)
                polygons.erase(polygons.begin() + i);
        }
    }
    return 0;
}

END

完整的代码可以点击这里