前言
虽然现在深度卷积神经网络在计算机视觉领域表现的非常优秀，但它在大型数据集上训练时需要花费大量GPU计算时间，并且前向推理需要大量的计算力。我们希望深度卷积网络可以在嵌入式平台部署，并且希望在保证精度的情况下加快它的推理速度。常规的基于FFT的卷积对于大型滤波器是快速的，但是现有技术的卷积神经网络一般使用小的3×3滤波器。论文引入了基于Winograd的最小滤波算法，一种新的卷积神经网络快速算法。算法在小卷积上计算复杂度最小，这使得它在滤波器和batch小的情况下更快。论文使用VGG网络对算法的GPU实现进行基准测试，并展示了批处理大小从1到64的时时吞吐量。[1]
Cong和Xiao使用Strassen算法进行快速矩阵乘法，以减少卷积网络层中的调度次数，从而降低其总算术复杂度。 作者还提出，来自算术复杂性理论的更多技术可能适用于衔接。
原始的Winograd算法，前置了很多数论方面的知识，为了效率我就没有深入的去阅读了。本文主要针对阅读了Fast Algorithms for Convolutional Neural Networks。
卷积公式
假设卷积为G，图像为D，输入参数数量N，通道C，高H，宽W
卷积核参数通道C，高R，宽S，则卷积公式如下
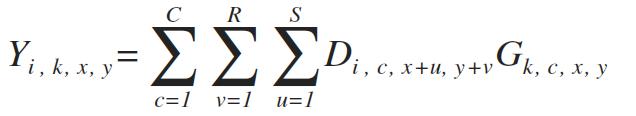
我们可以将整个图像的输出写作（其中*指代2D相关性）
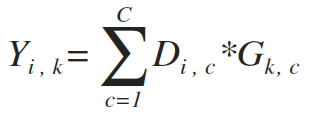
算法
假设用长度为r的FIR滤波器来得到输出m的式子为，传统的winograd算法需要次乘法。我们可以通过堆叠一维算法来得到二维的最小算法——假设指代用的滤波器来计算得到的输出，则它需要
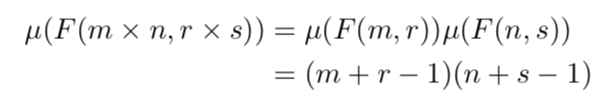次乘法。以此为例，我们可以继续堆叠一维算法来得到多维的最小算法。
但是需要注意不管是一维、二维还是多维的最快计算法，它要求输入的数量与所需乘法数一样。
我们知道，乘法和加法在硬件实现上的时间复杂度一般是不一样的，乘法运算所需的时间通常远大于加法所需的时间。因此，用廉价运算代替昂贵运算也是加速运算的一种方法。原始的矩阵运算对于需要6次乘法，而Winograd提出了如下算法，
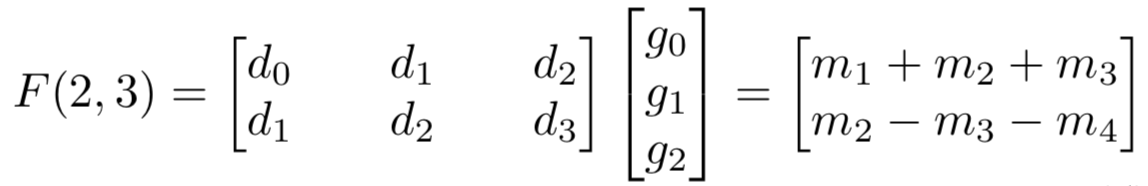其中，
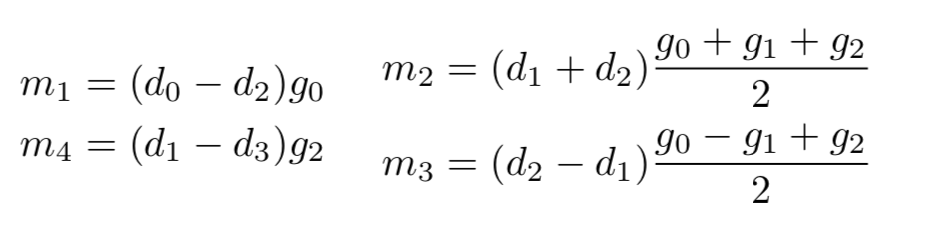
该算法只用了个乘法就计算得到了，不过它涉及了4个与输入数据有关的加法，还有与常数滤波器有关的3个加法（只要算一次就行了）和2个乘法（因为滤波器为常数，所以这3个加法和2个乘法可以认为不占用时间）。
我们可以将矩阵公式写成
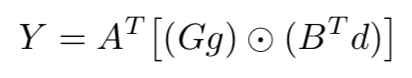其中，指逐元素的乘法（就是点乘，卷积用的）。对于而言，上述公式各元素表示的意义如下
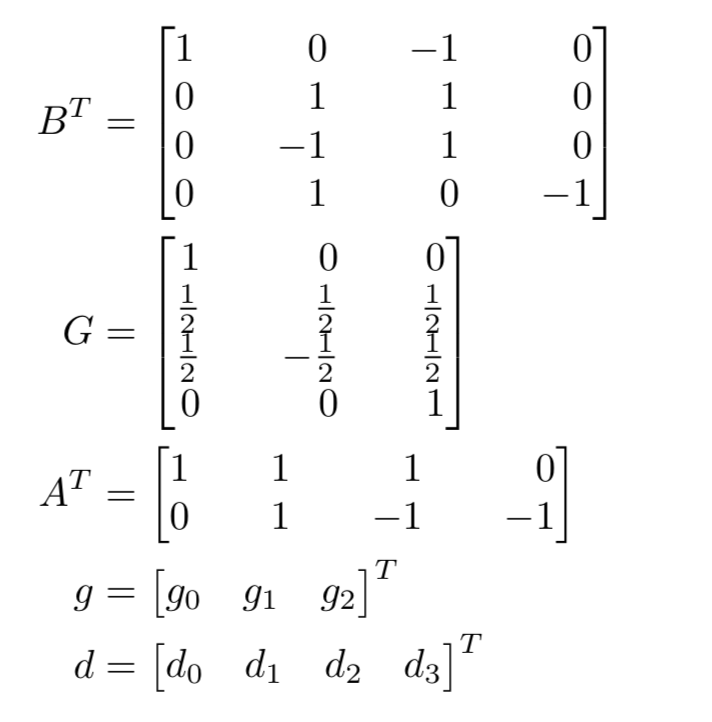
堆叠一维算法可以得到二维算法如下（这一步论文没有具体的分析，不是很懂为什么，估计是各种线性变换(￣▽￣) ）
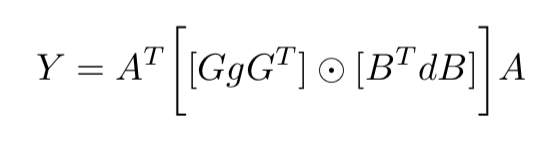其中，是一个的滤波器，是一个的输入图像块。
用winograd只需要次乘法，而原始矩阵运算则需要次乘法运算。尽管winograd法还需要用32次加法来进行数据转换，用28个浮点运算指令来进行滤波器转换，用24次加法来进行反转变换，但是相比原始矩阵运算法还是提升很大。
可以被用来计算卷积核为的卷积操作。其中，输入图像的每个通道需要被切割成大小的块（每个块与相邻块间有的重叠区域），则每个通道可以有个块。然后可以分别计算所有块然后累加得到最终结果。
假设和，则
以为各个块坐标，指单张图片，为滤波器，则可以将上述卷积公式改写成，
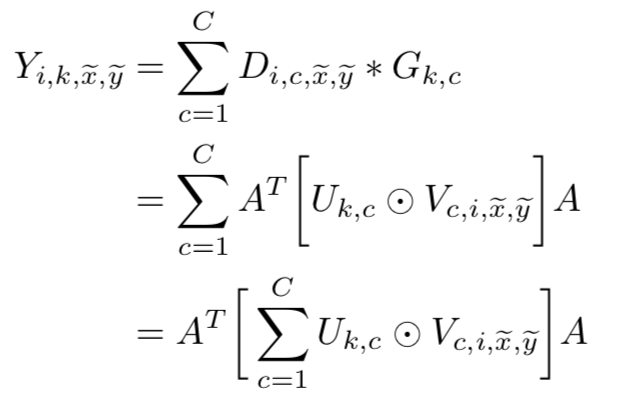
以下是具体实现的伪代码
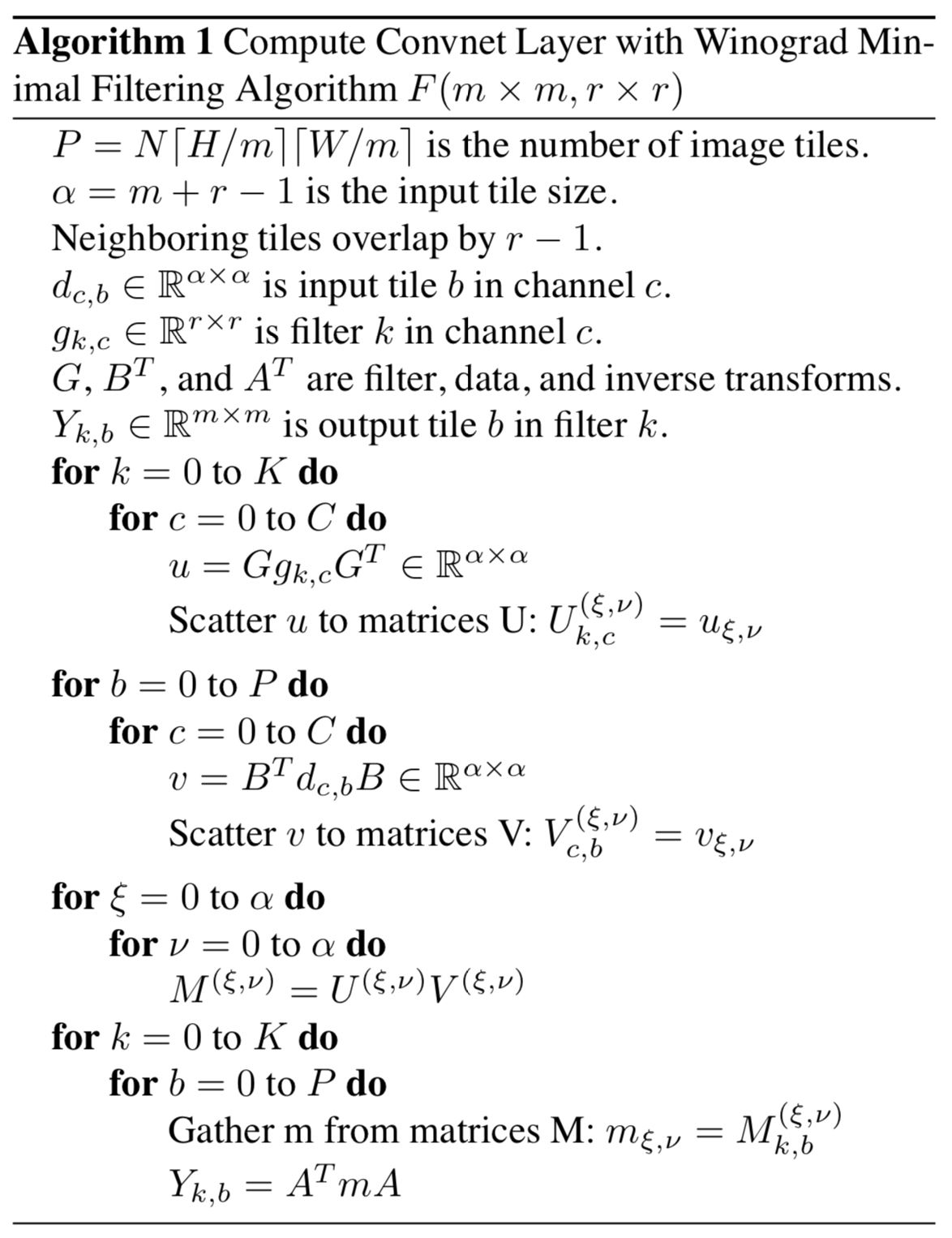
论文接下来的算法介绍主要提供了和的矩阵。
理解
下面这个公式是最重要的一块。
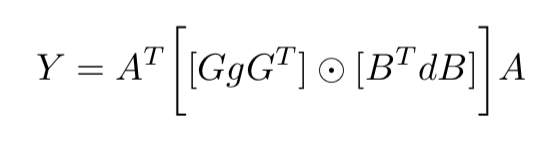
根据不同的卷积核有不同的值，而且是提前计算好的，可以用https://github.com/andravin/wincnn的脚本计算。不过，也不是可以通过脚本直接得到的，还需要自己确定个插值点，wincnn的作者推荐了https://openreview.net/forum?id=H1ZaRZVKg¬eId=H1ZaRZVKg可以帮助确定插值点。（感觉好难啊（−＿−；））
自己推了好久，发现根本就没办法算，之后只能找代码看（winograd.py），原来winograd是一定要加padding补全的，加多少padding视情况而定。所以其实这个算法就是针对卷积套公式，不过卷积计算选择不同算法，速度会不太一样。（现在有许多版本的winograd）
对于不同的输入用不同的padding补全，最后会选择性地舍弃部分数据。如的输入，在用计算时，会在左边补一个padding，在右边补两个padding，最后winograd卷积得到一个的输出，这时就要舍弃最右边的一列。
我尝试写了一下自己版本的winograd算法，以便后面学习优化，具体可以看下一篇。
参考文献